En matemática, la integración de una función no negativa, en el caso más simple, puede ser mirada como el área bajo la gráfica de una curva y el eje x.
La integral de una función f entre los límites de integración a y b pueden ser interpretados como el área bajo la gráfica de f.
Esto es fácil de entender para funciones que nos son familiares como los polinomios, la exponencial o logarítmica.
Nos planteamos el siguiente problema: ¿Como podemos calcular el area comprendida entre las rectas verticales de ecuaciones x=a y x=b, la grafica de la funcion 'f' y el eje 'x'? El área que queremos calcular corresponde a la superficie coloreada de azul en la figura de abajo:Este area es el valor de la integral
entre a y b de f y la denotamos por:
Esta integral se trata de una integral definida. Una integral definida es, por tanto, un número, mientras que una integral definida es una familia de funciones ( el conjunto de primitivas de la función que se integra ).Asi cuando n=2:
uno podria esperar que la aproximación obtenida sea peor que si se considera un número mayor de rectangulos, por ejemplo n=4
Entonces sii llamamos Sn a la suma de los rectangulos, se tiene que:
Fuentes:http://www.educared.org/wikiEducared/%C3%81rea_bajo_la_grafica_de_una_funci%C3%B3n_continua.html
http://www.mitecnologico.com/igestion/Main/AreaBajoLaGr%E1ficaDeUnaFunci%F3n


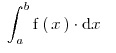




No hay comentarios:
Publicar un comentario