En esta unidad se estudiaran las aplicaciones de la integral.
El subtema 3.1 abordara las áreas generadas en la integración de funciones y se abordaran:el área bajo la gráfica de una función, asi como el área entre las gráficas de funciones.
El subtema 3.2 fundamentara la longitud de arco de una curva, también llamada rectificación de una curva y que es la medida de la distancia o camino recorrido a lo largo de una curva o dimensión lineal.
En el subtema 3.3 se vera el calculo de volúmenes de sólidos de revolución, ejemplificando el metodo del disco, el Método de la arandela y el Método de los casquillos cilíndricos
En el subtema 3.4 veremos lo referente al calculo de funciones.
Para finalizar el subtema 3.5 tratara de reforzar el tema general con otras aplicaciones de la integral, como lo es la longitud de una curva, la integracion numerica, etc..
Fuentes de imagenes:
http://analisisfigempa.wikispaces.com/file/view/Dibujo86.JPG/193459908/Dibujo86.JPG
http://www.cidse.itcr.ac.cr/cursos-linea/CALCULODIFERENCIAL/curso-elsie/aplicacionesintegral/html/images/imagen19ab.gif
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg7Vk0NVBK2FapCKibjsqMTCflu0BSDN81tli7ehiV8WO7WW_cFdUR6J-Q-pIxrmBG91LiDThIpBdgSi024xTDfKpjzEVCQtqd7gDY4MUD6slIiBFAsFou7sZkdKq93ktyU0wLqm5Ccld0/s320/funciones.png
http://www.todomonografias.com/images/2007/02/100590.gif









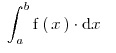

























 tal que se conozca su condición, tal como la divergencia para la serie geométrica con razón (en valor absoluto) mayor que 1, |z| > 1. Entonces:
tal que se conozca su condición, tal como la divergencia para la serie geométrica con razón (en valor absoluto) mayor que 1, |z| > 1. Entonces: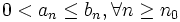
 converge
converge diverge
diverge  diverge
diverge
 converge
converge  converge
converge y
y 
 , tal que
, tal que 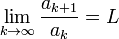
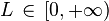 , el Criterio de D'Alembert establece que:
, el Criterio de D'Alembert establece que: converge si y sólo si
converge si y sólo si  es finita.
es finita.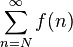
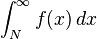
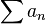 una serie monótona de números positivos decrecientes.
una serie monótona de números positivos decrecientes.  converge si y sólo si la serie
converge si y sólo si la serie converge
converge